2 Capítulo Métricas

Carregar os pacotes necessarios:

library(tidyverse)
library(sf)
library(terra)
library(eprdados)
library(landscapemetrics)

2.1 Pergunta 1

Descreva brevemente 2 métricas de cada nível (patch, class, landscape) usando ajudar (usando ? e/ou list_lsm), aulas ("Métricas da paisagem: Modelo mancha-corredor-matriz" e "Índices de Paisagem e Análises de Padrões Espaciais" ) e/ou a leitura disponivel no Google Classroom (Base teórica 4 Dados, métricas, analises). Incluindo na descrição - o nome, porque serve, unidades de medida, e relevância ecológica.

2.1.1 resposta

Para responder a pergunta você deve revisar as aulas e o conteúdo no capitulo Métrica. Métricas (descrição - o nome, porque serve, unidades de medida, e relevância ecológica) para todos os níveis foram apresentadas nas aulas “Métricas da paisagem: Modelo mancha-corredor-matriz” e “Índices de Paisagem e Análises de Padrões Espaciais”. Exemplo com uma métrica tamanho (área):

Nível de mancha - tamanho da mancha.
Nível de classe - tamanho média das manchas.
Nível de paisagem - tamanho média das manchas.

Podemos verificar as métricas disponíveis no pacote landscapemetrics com o seguinte código:

# ajudar para entender a função
?landscapemetrics::list_lsm

# Nível de mancha
landscapemetrics::list_lsm(level = "patch", 
                           type = "area and edge metric")

# Nível de classe
landscapemetrics::list_lsm(level = "class", 
                           type = "area and edge metric")

# Nível de paisagem
landscapemetrics::list_lsm(level = "landscape", 
                           type = "area and edge metric")

# todos as métricas com area
landscapemetrics::list_lsm(metric = "area")

# detalhes sobre a métrica (unidade etca)
?landscapemetrics::lsm_p_area

2.2 Pergunta 2

O modelo mancha-corredor-matriz é frequentemente adotado na ecologia da paisagem. Com base nas aulas teóricas e usando os valores no objeto minha_amostra_1000 apresentados na tabela acima, identificar qual classe representar a matriz na paisagem. Há alguma informação faltando que limita a sua capacidade de identificar qual classe representar a matriz? Se sim, o que precisa ser adicionado? Justifique as suas respostas de forma clara e concisa.

2.2.1 resposta

Para responder a pergunta você preciso entender a definação da “matriz” no contexto de Ecologia da Paisagem - modelo de mancha-corrredor-matriz (aula - Métricas da paisagem: Modelo mancha-corredor-matriz). Neste caso, class 0 é o classe dominante - com a área core cobrindo quase 67% da paisagem. Assim sendo, classe 0 e a matriz. Não há necessidade de informações adicionais. Se os valores estivessem menores e mais próximos (por exemplo, 41 e 44%), provavelmente precisaríamos incluir métricas adicionais para representar padrões espaciais na paisagem, como coesão, tamanho do maior mancha etca.

2.3 Pergunta 3

Em vez de extensão, você preciso incluir o tamanho (área do circulo) correspondente a cada raio. Incluir uma cópia do código ajustado para produzir uma figura com tamanho (área em quilômetros quadrados) no eixo x.

2.3.1 resposta

Seguindo o exemplo do capítulo, sabemos que os buffers têm formato de círculo, potanto:

A extensão seria o diametro da buffer (raio x 2).
Sabemos que a área de um círculo é pi vezes o raio elevado ao quadrado. Portanto, estimar a área do buffer em metros quadrados: pi X (raio ²).
E para finalizar converta o valor da área em quilômetros quadrados.

No R, podemos fazer isso, ajustando o codigo no capítulo com a função mutate(). Usamos mutate() para fazer novas colunas com o valor da área em metros quadrados area_m2 e quilômetros quadrados area_km2. Mantemos os nomes curtos, e depois atualize o rótulo do eixo para refletir a nova coluna com valores de área, especificando o nome do eixo x com a função labs().

amostras_metrica |> 
  filter(class==1) |> 
  mutate(ext_m = 2*raio, 
         area_m2 = 3.14*(raio^2)) |> 
  mutate(area_km2 = area_m2/1000000) |>
  ggplot(aes(x = area_km2, y = value)) + 
  geom_point() + 
  geom_line() +
  labs(x = "Área (quilômetros quadrados)", 
       y = "Área central de floresta\n(porcentagem da paisagem)") + 
  theme(text = element_text(size = 14))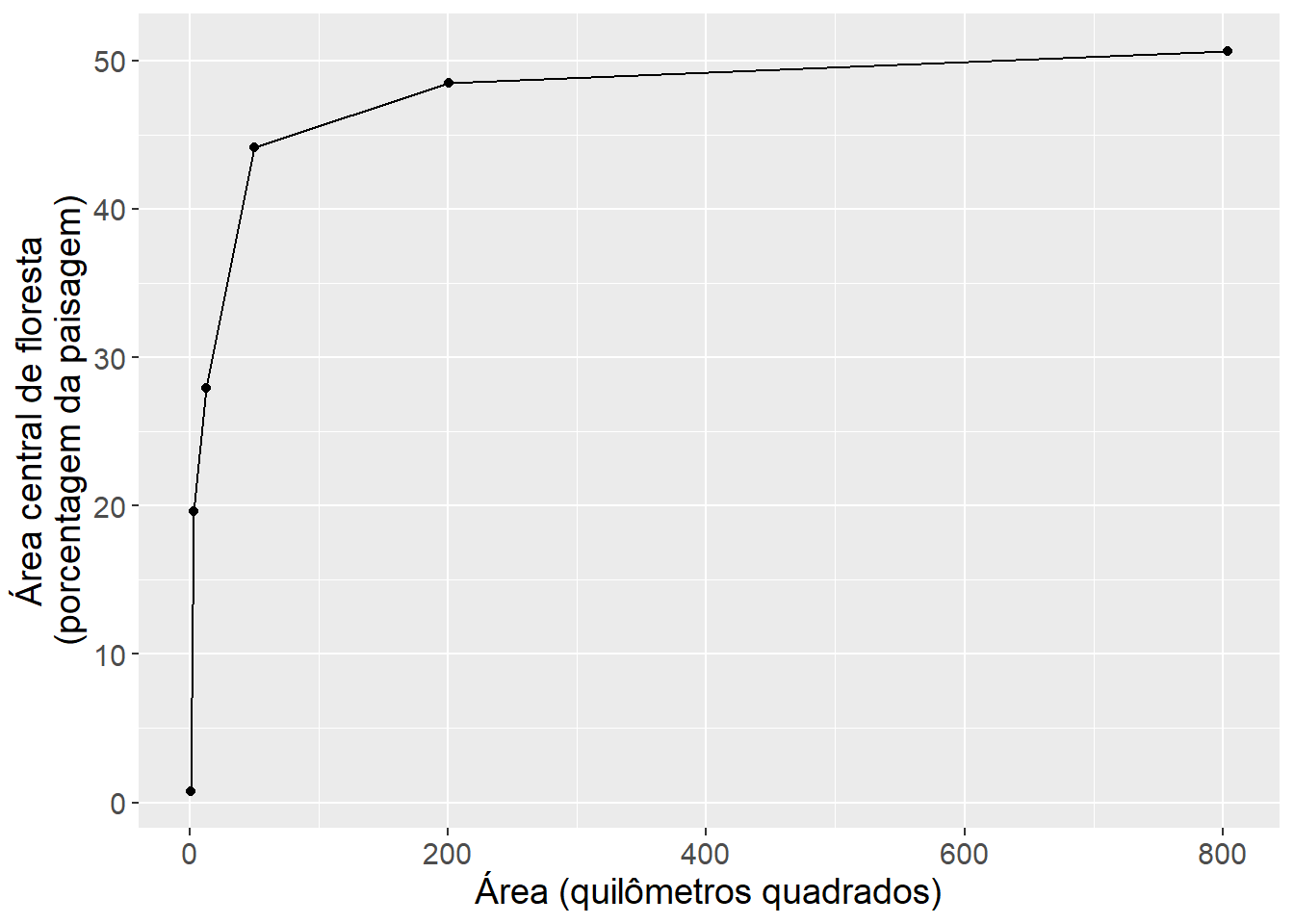

2.4 Pergunta 4

Por que é melhor usar métricas como proporção da área central (proportion of core area) para comparações multiescala na ecologia da paisagem? Inclua uma comparação com outras métricas, como área de mancha (patch area), para ilustrar por que as métricas expressas como proporção são mais apropriadas para comparações multiescala. Justifique a sua resposta de forma clara e concisa (menos de 500 palavras). Apoie sua resposta com exemplos da literatura científica.

2.4.1 resposta

Existem vários motivos para escolher a métrica. A resposta deve ser baseada nas aulas e na literatura sugerida e deve incluir algumas das seguintes considerações.

Embora métricas como área de mancha possam ser informativas, o uso de métricas expressas como proporções (como a proporção da área central) apresenta várias vantagens quando se trata de comparações multiescala:

Padronização em diferentes escalas:
- Área de mancha: A área de mancha absoluta é irrelevante quando se compara em diferentes escalas. A área de mancha possível aumenta com a escala - não é possível ter uma mancha de 1 km numa escala de 100 metros. Além disso, um fragmento florestal pode ser considerado grande em uma escala local, mas pequeno em uma escala regional. Isso torna as comparações multiescala baseadas em valores absolutos de área não confiáveis.
- Proporção da área central: Expressa como proporção da paisagem total, ela padroniza a área central independentemente do tamanho geral da paisagem.
Foco no habitat interior:
- Área de mancha: Essa métrica captura o tamanho total de um mancha, incluindo suas bordas. Os habitats de borda geralmente experimentam condições microclimáticas e pressões ecológicas diferentes em comparação com o interior.
- Proporção da área central: Ela isola o habitat interior excluindo uma zona de amortecimento da borda com base em uma profundidade específica (por exemplo, 30m). Isso concentra-se no habitat mais crucial para espécies sensíveis aos efeitos de borda, fornecendo uma comparação mais relevante do ponto de vista ecológico.
Aplicabilidade a diferentes tipos de paisagem:
- Área de mancha: Seu apelo universal pode ser enganoso, pois sua interpretação varia dependendo do tipo de paisagem. Uma pequena área pode ser significativa em uma paisagem agrícola fragmentada, enquanto uma grande área pode ser menos significativa em uma paisagem florestal mais contínua.
- Proporção da área central: A expressão relativa a torna mais aplicável a diferentes tipos de paisagem e permite comparações mais conscientes do contexto. Exemplo: Imagine comparar duas paisagens: um pequeno parque urbano com um fragmento florestal de 100 hectares e um grande parque nacional com um área central florestal de 10,000 hectares. Ambos têm a mesma proporção da área central (10%), indicando disponibilidade de habitat interior semelhante para espécies dependentes da área central. No entanto, suas áreas de mancha absolutas seriam drasticamente diferentes e forneceriam uma comparação multiescala potencialmente enganosa.

No geral, a proporção da área central emerge como uma métrica mais robusta e informativa para comparações multiescala na ecologia da paisagem. Seu foco no habitat interior e aplicabilidade em diferentes escalas a tornam uma ferramenta valiosa para entender a importância ecológica das padrões espaciais e heterogeneidade nas paisagens em diferentes níveis de detalhe. Embora a área de mancha é talvez a mais importante de todas as métricas, é crucial reconhecer suas limitações quando se busca comparações informativas e robustas em diferentes escalas.

Aqui estão alguns exemplos específicos de como a proporção da área central pode ser usada para comparações multiescala na ecologia da paisagem:

Comparação da conectividade entre paisagens:
A proporção da área central pode ser usada para comparar a conectividade entre paisagens em diferentes escalas. Por exemplo, a proporção da área central de corredores ecológicos pode ser usada para comparar a conectividade entre fragmentos florestais em diferentes escalas espaciais.
Comparação da diversidade de habitat:
A proporção da área central pode ser usada para comparar a diversidade de habitat entre paisagens em diferentes escalas. Por exemplo, a proporção da área central de diferentes tipos de habitat (as classes categóricas em um raster) pode ser usada para comparar a diversidade de habitat em diferentes escalas espaciais.

2.5 Pergunta 5

Em menos de 200 palavras apresente a sua interpretação do gráfico em figura 2.4.

2.5.1 resposta

A proporção de floresta muda com a escala espacial, representado pela extensão do buffer em torno do ponto amostral. Existe uma relação positiva entre o percentual de área central e a extensão. A proporção de floresta aumenta de zero a 51 por cento, mas a relação não é linear. Os valores aumentam rapidamente até extensões de 8 km (6% por quilometro em média entre 0 e 8 quilômetros). Após isso a curva parece atingir uma assíntota (aumentando 0.25% por quilometro entre 8 e 16 quilômetros).

2.6 Pergunta 6

Comparar os resultados apresentados nas figuras com modelos lineares e não-lineares. Como podemos estabelecer qual seria o melhor modelo? Qual modelo seria mais adequado para identificar limiares no padrão de área central de floresta?

2.6.1 resposta

Uma inspeção visual sugere que um modelo linear sem qualquer transformação tem os maiores intervalos de confiança e é o pior modelo. Um modelo linear com dados transformados parece ajustar-se proximo aos dados. O modelo não linear mostra melhor os padrões nos dados originais. Mas essas avaliações são subjetivas. Deveríamos realizar testes estatísticos para confirmar estas avaliações visuais. Todos os modelos melhorariam (por exemplo os intervalos de confiança ficariam menores) se aumentássemos o tamanho da amostra calculando a métrica com mais distâncias de buffer.

2.7 Pergunta 7

Aumentar o tamanho amostral na analise. Usando os exemplos de codigo anteriores, aumentar o numero de buffers entre 125 m e 16 km. i) Calcular a metrica cpland para 12 distâncias de bufferes e montar dados novas (isso é cinco distâncias novas e as sete distâncias originais) em um objeto com nome de "amostras_metrica_nova". ii) usando ggplot2 fazer um gráfico com os novos dados mostrando valores de extensão no eixo x e proporção da floresta central no eixo y. Ajustar o codigo para incluir intervalos de confiança junto com o modelo linear. Comparar os resultados apresentados nas figuras com modelos lineares sem transformação. O que aconteceu com o ajuste do modelo e os intervalos de confiançã? Foi útil incluir mais distâncias? Justifique as suas respostas de forma clara e concisa. Inclua cópias do seu código e gráficos na sua resposta. Você pode usar o printscreen para mostrar o RStudio com seu código e gráficos.

2.7.1 resposta

Passos para desenvolver uma resposta:

Decida as distâncias para os cinco novos buffers.
Calcular a métrica nos novos buffers.
Adicione os novos dados junto com as setes distâncias originais.
Faça o gráfico.

Olhando o gráfico “Comparação de padrões lineares e não-lineares.” vemos que quando os pontos estão mais próximos os intervalos de confiança são menores. Os intervalos de confiança são maiores onde há maiores distâncias entre os pontos. Portanto, incluiremos mais buffers entre 1 e 16 quilômetros.

O código abaixo fará isso em R:

Lembrando o codigo para as buffers originais:

# raio 250 metros
sample_lsm(floresta_2020, y = rio_pontos_31976[1, ], 
           size = 250, shape = "circle", 
           metric = "cpland") |> 
  mutate(raio = 250) -> minha_amostra_250 
# raio 500 metros
sample_lsm(floresta_2020, y = rio_pontos_31976[1, ], 
           size = 500, shape = "circle", 
           metric = "cpland")  |> 
  mutate(raio = 500) -> minha_amostra_500
# raio 1 km (1000 metros)
sample_lsm(floresta_2020, y = rio_pontos_31976[1, ], 
           size = 1000, shape = "circle", 
           metric = "cpland")  |> 
  mutate(raio = 1000) -> minha_amostra_1000
# raio 2 km
sample_lsm(floresta_2020, y = rio_pontos_31976[1, ], 
           size = 2000, shape = "circle", 
           metric = "cpland") |> 
  mutate(raio = 2000) -> minha_amostra_2000
# raio 4 km
sample_lsm(floresta_2020, y = rio_pontos_31976[1, ], 
           size = 4000, shape = "circle", 
           metric = "cpland")  |> 
  mutate(raio = 4000) -> minha_amostra_4000
# raio 8 km
sample_lsm(floresta_2020, y = rio_pontos_31976[1, ], 
           size = 8000, shape = "circle", 
           metric = "cpland")  |> 
  mutate(raio = 8000) -> minha_amostra_8000
# raio 16 km
sample_lsm(floresta_2020, y = rio_pontos_31976[1, ], 
           size = 16000, shape = "circle", 
           metric = "cpland")  |> 
  mutate(raio = 16000) -> minha_amostra_16000

Podemos agora seguir o exemplo original e incluir novas distâncias (1,5km; 3km; 6km; 11km e 14km):

# novas buffers
# raio 1.5 km
sample_lsm(floresta_2020, y = rio_pontos_31976[1, ], 
           size = 1500, shape = "circle", 
           metric = "cpland")  |> 
  mutate(raio = 1500) -> minha_amostra_1500
# raio 3 km
sample_lsm(floresta_2020, y = rio_pontos_31976[1, ], 
           size = 3000, shape = "circle", 
           metric = "cpland") |> 
  mutate(raio = 3000) -> minha_amostra_3000
# raio 6 km
sample_lsm(floresta_2020, y = rio_pontos_31976[1, ], 
           size = 6000, shape = "circle", 
           metric = "cpland")  |> 
  mutate(raio = 6000) -> minha_amostra_6000
# raio 11 km
sample_lsm(floresta_2020, y = rio_pontos_31976[1, ], 
           size = 11000, shape = "circle", 
           metric = "cpland")  |> 
  mutate(raio = 11000) -> minha_amostra_11000
# raio 14 km
sample_lsm(floresta_2020, y = rio_pontos_31976[1, ], 
           size = 14000, shape = "circle", 
           metric = "cpland")  |> 
  mutate(raio = 14000) -> minha_amostra_14000

# juntar dados objeto novo com nome de "amostras_metrica_nova"
bind_rows(minha_amostra_250, 
          minha_amostra_500, 
          minha_amostra_1000,
          minha_amostra_1500,
          minha_amostra_2000,
          minha_amostra_3000,
          minha_amostra_4000,
          minha_amostra_6000,
          minha_amostra_8000,
          minha_amostra_11000,
          minha_amostra_14000,
          minha_amostra_16000) -> amostras_metrica_nova

Gráfico.

amostras_metrica_nova |> 
  filter(class==1) |> 
  mutate(ext_m = 2*raio, 
         ext_km = (2*raio)/1000) |>
# fazer o gráfico
  ggplot(aes(x = ext_km, y = value)) + 
  geom_point(size = 4) + 
  geom_line() +
  stat_smooth(method = "lm", se = TRUE, color = "green", 
              linetype = "dashed") + 
  labs(x = "Extensão (quilômetros)", 
       y = "Área central de floresta\n(porcentagem da paisagem)") + 
  theme_bw() +
  theme(text = element_text(size = 18))

`geom_smooth()` using formula = 'y ~ x'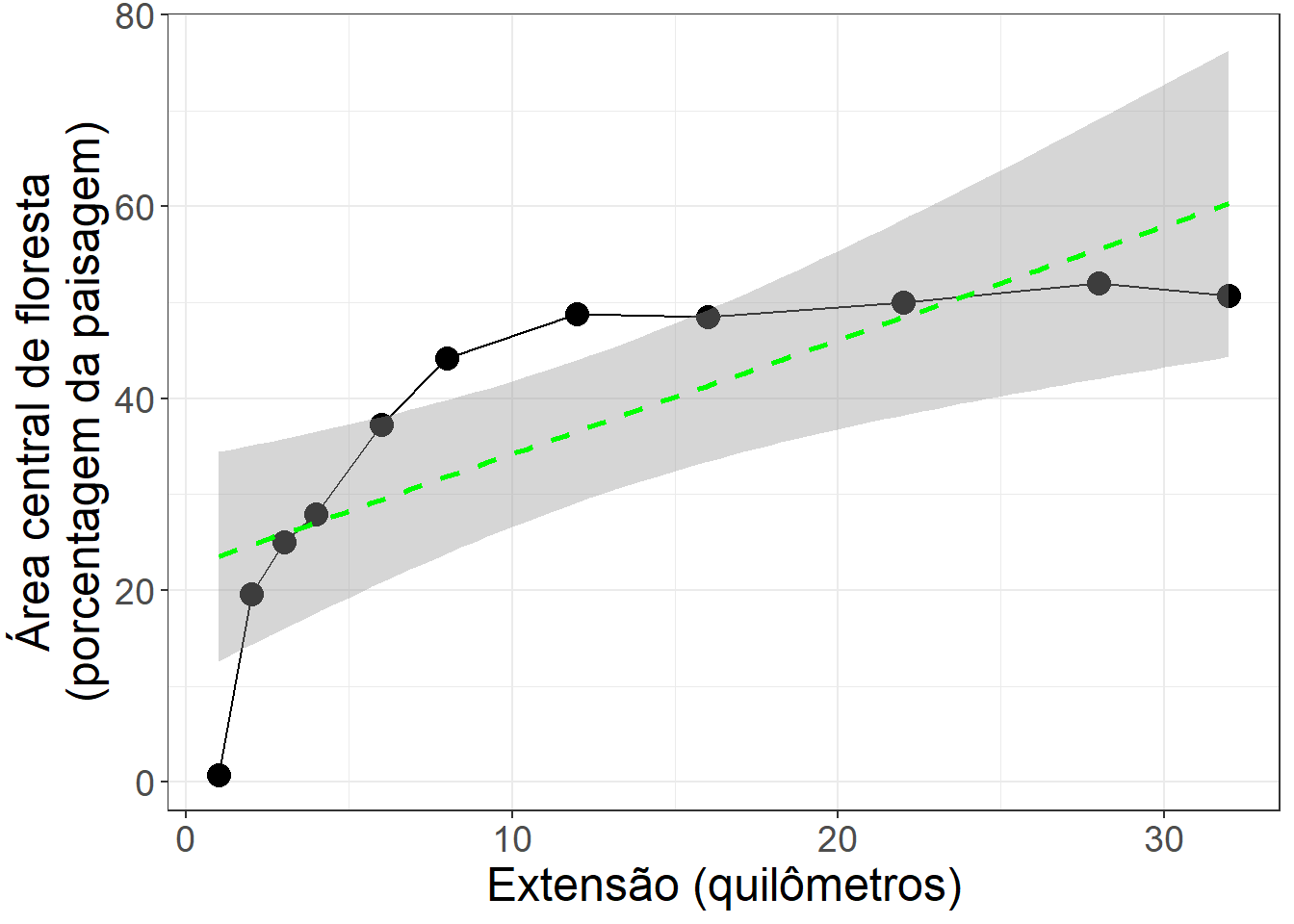

2.8 Pergunta 8

Com base nos resultados apresentados (figura e tabela) caracterisar as mudançãs na paisagem em função de extensões diferentes. Olhando os gráficos prever como seria o padrão para extensões maiores (lembrando que valores são doubrados - por exemplo raio de 250 metros gerar uma extensão de 500 metros). Seria relevante repetir incluindo calculos para extensões maiores (por exemplo 64 km e 128 km)? Justifique sua caracterização e previsões de forma clara e concisa, apoie sua escolha com exemplos da literatura científica.

2.8.1 resposta

2.9 Pergunta 9

Usando como base o conteudo das aulas, leitura disponivel no Google Classroom (Base teórica 4 Dados, métricas, analises), e/ou exemplos apresentados aqui no tutorial, selecione pelo menos oito métricas de nível classe para caracterizar a paisagem de estudo e objectivos da sua projeto em grupo. Justifique sua seleção de forma clara e concisa, apoie sua escolha com exemplos da literatura científica.